Key Takeaways
- Choosing the correct machine vision lens is vital for optimal performance. Understanding fundamental parameters like working distance (WD), field of view (FOV), and resolution is essential.
- This ensures that the lens meets specific application requirements. Whether fixed or zoom, lenses must align with the chosen camera. Equations like 1/f = 1/do + 1/di aid in determining focal lengths for simpler setups, while Equation 3 (shown below) streamlines lens selection for more complex systems.
- Fixed focal length lenses offer consistent performance at specified magnifications, which simplifies integration. Ultimately, careful consideration of these factors ensures the selection of the most suitable imaging lens.
How to Choose a Zoom Lens
When selecting a machine vision lens, we can choose from some common types of imaging lenses based on the application. To select an imaging lens more precisely, it is essential to understand the basic imaging system. At a minimum, we need to know the working distance (WD), field of view (FOV), and resolution before we can correctly select a lens. In this section, we assume that a camera has already been chosen, as this narrows down the selection range and makes it easier to choose a lens.
In our discussion, we can assume that fixed focal length lenses and zoom lenses operate on the same principles and can be selected in the same manner. Here, we assume that the zoom lens has been set at various focal lengths, and its zoom function has been locked.
In the actual selection process, factors such as the lens’s optical specification, mechanical dimensions, and cost must be considered. However, the focus will be on key specifications such as working distance (WD), field of view (FOV), and resolution. The working distance (WD) determines the distance between the lens and the subject, the field of view (FOV) determines the area the lens can cover, and the resolution determines the level of detail the lens can capture within the given field of view.
Therefore, when selecting a lens, it is necessary to ensure that it meets the specific application’s requirements for working distance, covers the required field of view, and provides sufficient resolution to capture the necessary details. By carefully considering these factors and adjusting them according to the specific needs of the application, you can ensure the selection of the most suitable imaging lens, thereby achieving optimal visual performance.
Image Formation by Thin Lenses
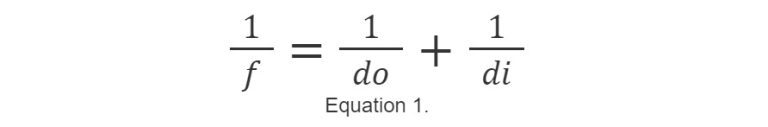
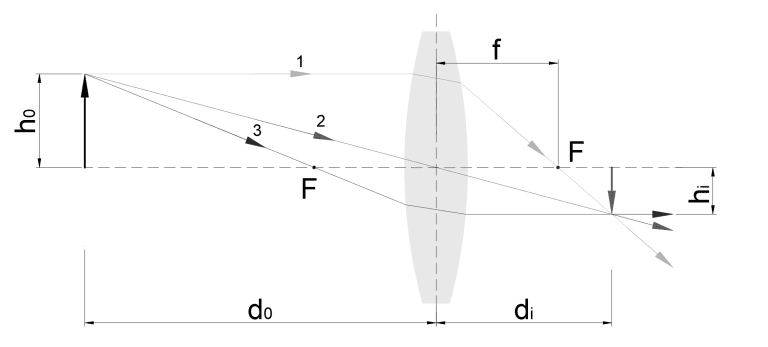
In the given equation1, (di) represents the image distance, which is the distance from the image plane to the last lens element. (d0) is the object distance, which is the distance from the object to the front lens element. The focal length of the lens is (f). This equation assumes that all values (di), (d0) and (f) are positive and that the lens is effectively thin, with no significant thickness affecting the optics. This simplification is used to demonstrate the inverse relationship between the object distance and the image distance: as the object distance increases, the image distance decreases, provided the focal length remains constant.
This equation is beneficial for determining the correct focal length for simple lens systems, like single plano-convex or bi-convex lenses, when the distances of the object and image are known. However, this equation is not comprehensive enough for complex machine vision systems with multi-element lenses. It doesn’t take into account the field of view (FOV), and because it’s not feasible to measure the image distance in such systems, this equation cannot be used to directly determine the focal length for these more intricate setups. Where hi and ho are the size of the image plane (most often a sensor size) and FOV respectively, Equation 1 can be rearranged into a more useful form, shown in Equation 3.
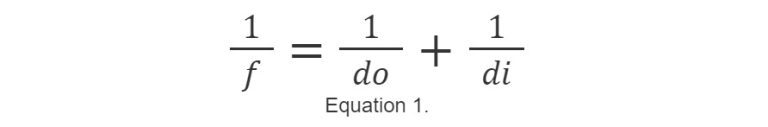
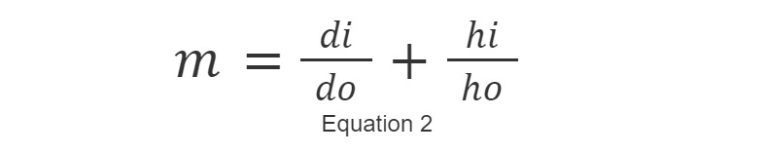
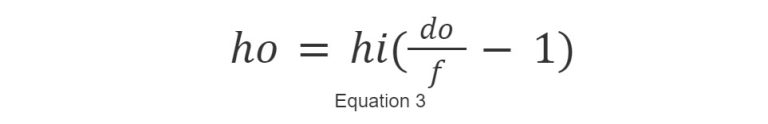
Equation 3 provides a quick and easy way to solve for which focal length lens is required to solve an application, given fundamental parameters such as FOV and sensor size.
The fundamental premise for using equation 3 in lens selection is the pre-selection of the camera, leaving the focal length ( f ) as the sole variable to determine the suitable lens. This simplifies the lens selection process significantly. Online lens calculators typically employ a variation of Equation 3 to provide their recommendations. It’s important to note that these are preliminary calculations and may not be accurate for lenses with significant distortion or those that do not conform to the thin-lens approximation.
Such graphical representations are valuable initial tools for narrowing down lens options for a specific application. However, they are not definitive guides for narrowing down some of the other critical characteristics of an imaging lens, such as image quality, distortion, or relative illumination. Their primary function is to establish the relationship between the field of view (FOV) and the sensor size.
How to Choose a Fixed Focus Lens
Generally speaking, lens types like telecentric or microscope objectives may appear daunting to integrate into an imaging setup due to their non-traditional behavior compared to fixed focal length lenses. However, the selection process is actually simpler for them than for a traditional lens.
With some exceptions, fixed magnification lenses typically operate optimally at a specific working distance (WD) and are characterized by their magnification. Since their magnifications are physically labeled on the lenses, they consistently perform at those magnifications, and their field of view (FOV) can be easily determined by equation 4.
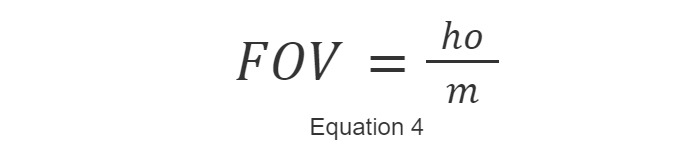
Where m is the magnification specified for the lens and ho is the sensor size. This equation shows that regardless of the sensor size, the magnification will remain the same; only the FOV changes.
Since this is a measurement application, a telecentric lens should be chosen with that magnification.
Related Content
GREAT ARTICLE!
Share this article to gain insights from your connections!



