Forgetting the Diffraction Limit: Avoid Optical Pitfalls Part 2

Key Takeaways

The diffraction limit is the fundamental resolution limit of an optical system, dictated by the wave nature of light and diffraction.
When light passes through an aperture, it forms an Airy disk—a central bright spot surrounded by rings. The smallest focusable point, or minimum spot size, is defined by this disk.
Calculated as Ra = 1.22λ/2Na, the radius depends on the light’s wavelength and the aperture size.
Resolution is limited when Airy disks overlap; further aperture increase can’t enhance it beyond the diffraction cutoff frequency.

There’s a mistake people often make when assessing the performance of a microscope or telescope— forgetting the diffraction limit. The diffraction limit is a theoretical limiting factor governing the maximum obtainable resolution of an optical system. When we leave it out of our calculations we may end up with very unrealistic expectations.

This article— part two of our series on “Avoid Optical Pitfalls”— will look at what the diffraction limit is, how to calculate it, and how it can affect the resolution of high performance optics.

What is the Diffraction Limit?

The diffraction limit is essentially the resolution limit that is imposed on an optical system by the wave nature of light and the process of diffraction. To understand this, let’s look at what diffraction does when light shines through an opening.

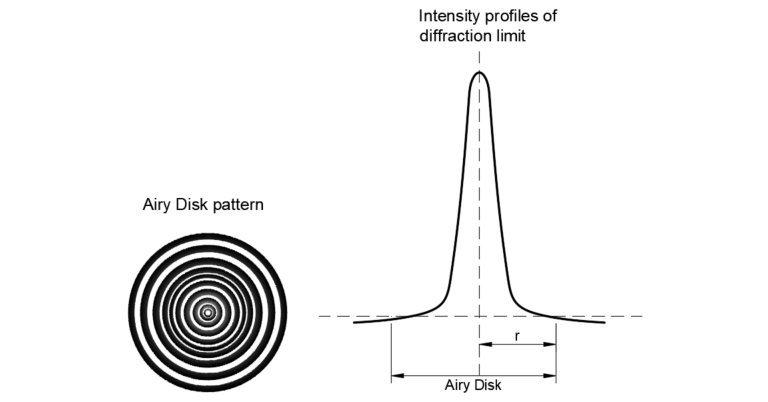
Any lens has a finite aperture, and when light passes through an aperture— no matter its size— diffraction will occur. We call a diffraction pattern an Airy disk, and it is disk shaped. There is a bright area in the center surrounded by concentric rings, and each ring decreases in brightness as you move out. This Airy disk is the key to the diffraction limit, as it is the Airy disk which is the smallest point to which you can focus a beam of light. We sometimes call this the ‘minimum spot size’ of an optical system.

The radius of the Airy disk depends on two important factors: the wavelength of light and the size of the aperture, and we can estimate it with the equation: Ra = 1.22λ/2Na. In this equation Ra is the airy radius, λ is the wavelength of illuminating light, and Na the numerical aperture.

As the numerical aperture increases, the radius of the airy disk decreases. In modern optics, the numerical aperture can be as high as 1.4-1.6. The table below shows the diameter of an airy disk for lenses of different apertures when the lens is illuminated with light at 520 nm.

f/#	Airy Disk Diameter [μm] at a Wavelength of 520nm
2	2.54
4	5.08
6	7.61
8	10.15
10	12.69
12	15.23

f/#	Airy Disk Diameter [μm] at a Wavelength of 520nm
2	2.54
4	5.08
6	7.61
8	10.15
10	12.69
12	15.23

Diameters of airy disk when lenses of various apertures are illuminated with green light.

Diffraction Limit and Resolution

How does this relate to the diffraction limit? Imagine a perfect lens with no aberrations, not limited by design or manufacturing flaw. Each point light source will create an airy disk, and when an image is properly resolved the airy disks do not overlap. When the outer rings merge, the sensor will be diffraction limited. The only way to improve resolution will be to increase the numerical aperture. But when the center of each airy disk merges, we’ve reached the limit of resolution; the diffraction cutoff frequency. When you’ve reached the limit of resolution you’ll not be able to resolve further even by increasing aperture.

What is the cutoff frequency of the lens, the diffraction limit? We can calculate it using the same two parameters we used to calculate the radius of our airy disks. The equation is:

Diffraction limit = 2Na/λ x (1000 μm/ 1 mm)

FAQ:

Can optical telescopes provide diffraction limited images in astronomy?

No; the passage of light through the atmosphere introduces significant distortions that limit performance to a lower resolution than provided by diffraction-limited observation.

Can the diffraction limit be improved upon?

No, since the diffraction limit is a direct consequence of the wave nature of light, it cannot be improved upon.

What are the implications of the diffraction limit?

The diffraction limit tells us that there is a limit to the resolution of images we can obtain, no matter how much we improve our optical system. Although this limit is not important for everyday photography or situations in which resolution is already limited by other significant optical aberrations, it is important to microscopy, telescopic, and high resolution photography.

What is the typical diffraction limit in microscopy?

For visible light microscopy, the diffraction limit— the smallest detail that can be resolved— is about 200-250 nanometers.

What is the diffraction limit in visible light telescopes?

For visible light telescopes, the diffraction limit is typically about 0.1-1 arc seconds.