- Microscope objectives, vital for optical microscopy, come in two primary modes: finite conjugate and infinite conjugate. Infinite conjugate objectives, which project to infinity and require a tube lens, offer flexibility for incorporating optical components without sacrificing image quality, making them popular in scientific and industrial applications.
- Long working distance objectives are crucial, providing operational flexibility, collision avoidance, and suitability for diverse samples. Achieving high magnification involves trade-offs, balancing resolution, NA, and aberration correction.
- Other key indicators include working wavelength, field of view, and flat field objectives for clear imaging.
- These advancements underscore ongoing design evolution in microscope objectives to meet diverse research and production needs.
Infinitely Conjugate Long Working Distance Microscope Objectives
Microscope objectives are essential components in optical microscopes, serving to magnify and capture images of observed objects. They find applications in diverse fields such as biomedical research, precision detection, and semiconductor processing. Additionally, microscope objectives are employed independently in scientific research and industrial production, for activities such as atom capture and laser processing.
Microscope objectives employ two primary imaging modes: finite conjugate imaging and infinite conjugate imaging. Infinite conjugate objectives project images to infinity and necessitate the use of a tube lens for imaging assistance. The parallel light path between the infinite conjugate lens and the tube lens facilitates the incorporation of optical components, such as splitters and polarizers, without compromising imaging quality. This flexibility has made infinite conjugate lenses a mainstream choice in the market.
The evolution of microscope objectives, with a historical backdrop, underscores the ongoing importance of design and development. The demand for specialized non-standard lenses in scientific research and increasing requirements in various fields drive the development of objectives with better flat-field characteristics, chromatic aberration correction, and, notably, long working distances.
Long Working Distance
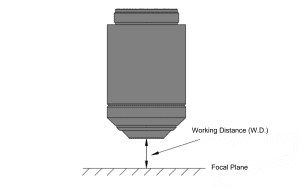
Working distance, denoting the distance between the object and the lens’s front end, emerges as a crucial parameter in microscope objective selection. Longer working distances afford greater flexibility in applications. For instance, in optical fiber fusion, a high-magnification objective with a long working distance improves alignment precision by providing ample space for the optical fiber.
Apart from operational flexibility, long working distances offer advantages such as collision avoidance between the sample and the objective, suitability for samples of varying thickness, and reduced risks of debris contamination and lens damage during processing. In specific scenarios like atom trapping and crystal growth observation, long working distance objectives become indispensable.
However, achieving long working distances often involves employing a reverse telephoto design structure, which increases lens diameter and complexity. This imposes higher requirements on optical design and lens processing capabilities.
Magnification = f tube /f objective
Resolution is expressed as a function of wavelength (λ) and numerical aperture (NA), with NA calculated as the product of the refractive index (n) and the sine of the half-angle (θ) of light from the object. Achieving high magnification often involves a trade-off, as increasing NA for better resolution concurrently poses challenges in correcting on-axis and paraxial aberrations and achieving long working distances. For an aberration-corrected objective that reaches the diffraction limit, the resolution is usually expressed as follows:Resolution=0.61*λ/NA
Where λ is the band and NA is the numerical aperture of the lens, which is the most commonly used aperture representation method for microscopic objective lenses:NA=n*sinθ
Where n is the refractive index of the medium between the lens and the object, and θ is the half-angle of the light from the object. The medium between a conventional lens and an object is air, called a dry lens, and the theoretical limit of NA is 1. If you want to break the theoretical limit, you need to change the medium to water or oil. Long working distance microscope objectives are usually dry lenses. High magnification means a short focal length, and short focal length can achieve large NA. Increasing NA is a common method to improve the resolution of objective lenses. As a small aberration optical system, a high NA means that more light is collected, but the light must be concentrated in a smaller area. With high NA as the premise, it is not easy to correct the on-axis and paraxial aberrations, and it is even more difficult to achieve long working distances at the same time.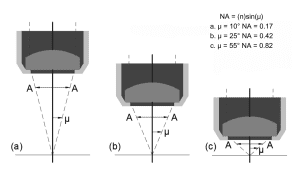
Key Concepts: Finite Conjugate
In the optical configuration of a finite conjugate system, light emanating from a light source, not positioned at infinity, converges to a specific spot (see Figure 11). In the context of a microscope, the image of the examined object undergoes magnification and is projected onto the eyepiece or camera sensor. The system’s particular distance is defined by either the DIN or JIS standard, with all finite conjugate microscopes adhering to one of these two standards. This design is prevalent in basic microscopes and finds application in scenarios where cost-effectiveness and simplified design are primary considerations.
Key Concepts: Infinite Conjugate *
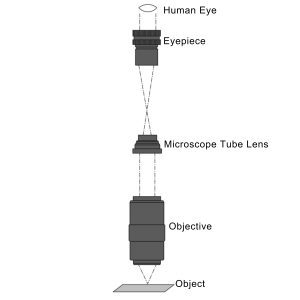
Contrastingly, in an infinite conjugate or infinity-corrected optical system, light originating from an infinitely distant source is focused on a small spot. Within an objective, this spot serves as the object under examination, while infinity points toward the eyepiece or camera sensor (refer to Figure 12). This sophisticated design incorporates an additional tube lens between the object and eyepiece, enabling the production of an image. Despite its complexity compared to finite conjugate designs, the infinite conjugate system allows the integration of optical components like filters, polarizers, and beamsplitters into the optical path. This feature facilitates advanced image analysis and extrapolation in complex systems.
For instance, the introduction of a filter between the objective and tube lens permits the observation of specific wavelengths of light or the blocking of unwanted wavelengths that might disrupt the setup. Fluorescence microscopy commonly employs this design. Another advantage of the infinite conjugate configuration is its capability to adjust magnification according to specific application requirements. The objective magnification is determined by the ratio of the tube lens focal length (fTube Lens) to the objective focal length (fObjective). By altering the tube lens focal length, typically a 200mm achromatic lens, the objective magnification can be customized. If an objective follows an infinite conjugate design, the objective body will bear an infinity symbol.
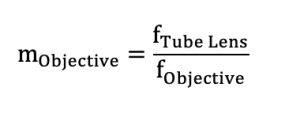
Other Important Indicators
Working Wavelength:
Different applications require different wavelengths. Microscope objective lenses typically operate in the visible light range, with a focus on chromatic aberration correction. Ultraviolet microscope objectives, designed for special purposes, contribute to improved resolution.Field of View: The area observable by the lens, the field of view, plays a crucial role. Flat field objectives, with minimal field curvature, ensure clear imaging across the entire observable area, a hallmark of high-end microscopic objectives.
Field of View:
The area observable by the lens, the field of view, plays a crucial role. Flat field objectives, with minimal field curvature, ensure clear imaging across the entire observable area, a hallmark of high-end microscopic objectives.
Conclusion
In conclusion, infinitely conjugate long working distance microscope objectives play a pivotal role in various scientific and industrial applications by providing high-resolution imaging capabilities. Their evolution highlights the constant need for advanced design and development to meet diverse research and production demands. Long working distances offer operational flexibility, collision avoidance, and suitability for various sample thicknesses, making them indispensable in critical scenarios like optical fiber alignment, atom trapping, and crystal growth observation.
Despite the challenges posed by achieving long working distances, the ongoing advancements in optical design and lens processing capabilities continue to push the boundaries of microscope objective performance, ensuring clear imaging and enhanced resolution for a wide range of applications.
GREAT ARTICLE!
Share this article to gain insights from your connections!


